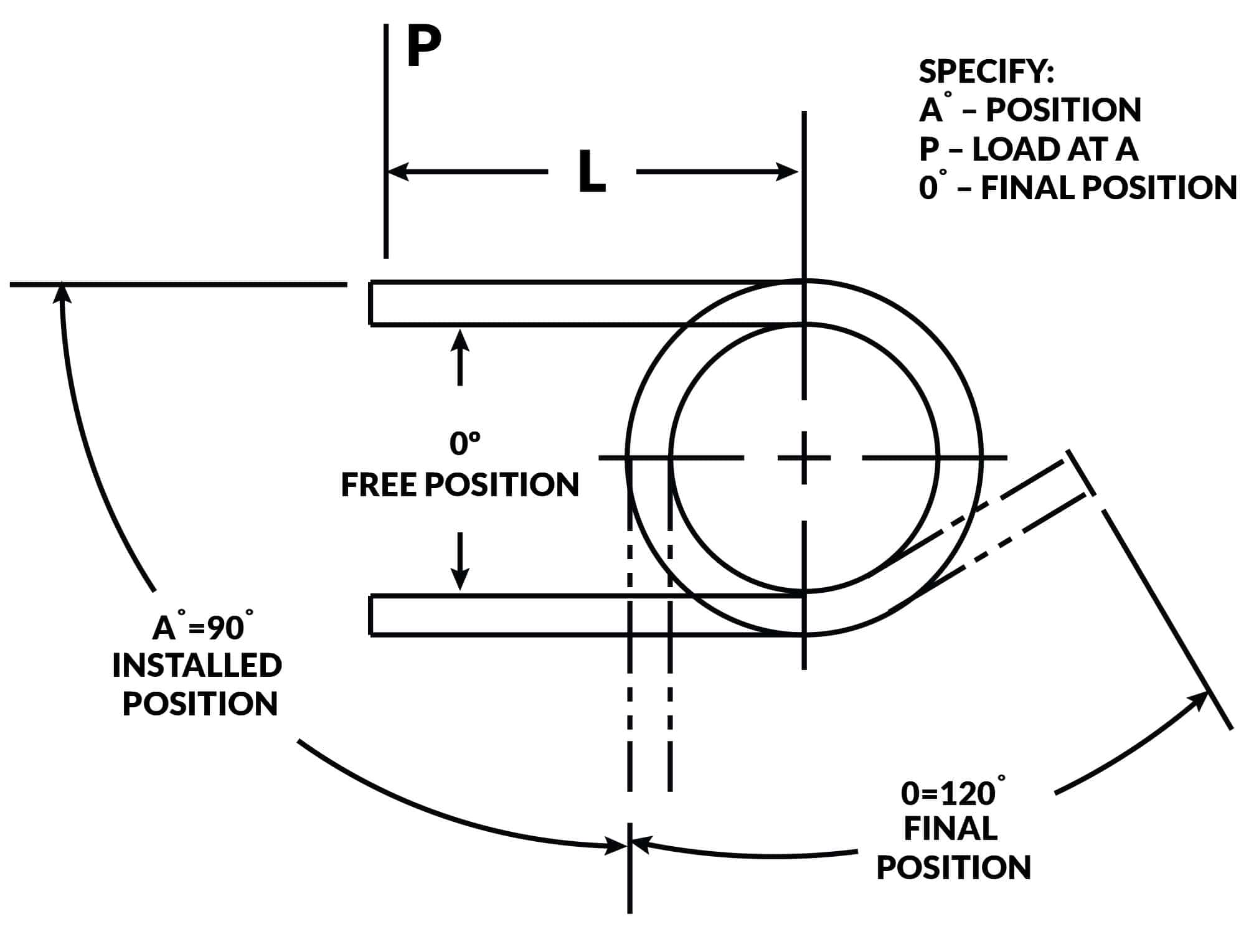
Get unique, complex parts easily. No matter your requirements, Chaoyi Spring creates hard-to-produce coil springs and wire forms.
Let us help you create the custom wire form you need, from S-hooks and J-hooks to utility hooks and more.
We work closely with customers across a wide range of industries, helping them design and manufacture made-to-order parts.
Why choose Chaoyi Spring? We prioritize customer-focused collaboration, modern equipment and the latest technology to make your parts per print.
Find the information and guidance you need, from measuring a spring to learning about materials, placing an order and much more.
Have you ever wondered about the fascinating world of springs and how they interact with objects? Imagine dropping a stone onto a spring – a simple yet intriguing scenario that


Have you ever wondered about the fascinating world of springs and how they interact with objects? Imagine dropping a stone onto a spring – a simple yet intriguing scenario that sparks a flurry of questions. How far will the stone compress the spring? What factors determine the extent of compression? Let's delve into the physics behind this seemingly straightforward event and uncover the intricate relationship between the stone's weight, the spring's stiffness, and the resulting compression.
At the heart of this phenomenon lies the interplay between gravity and the spring's elastic properties. When you drop a stone onto a spring, gravity pulls the stone downwards, creating a force that compresses the spring. The spring, in turn, resists this compression with a force of its own, known as the spring force. This force is directly proportional to the amount of compression, a principle elegantly articulated by Hooke's Law.
Hooke's Law states that the force exerted by a spring is directly proportional to its displacement from its equilibrium position. In simpler terms, the more you compress or stretch a spring, the stronger the force it exerts back. Mathematically, this is expressed as F = -kx, where:
The negative sign indicates that the spring force acts in the opposite direction to the displacement. When you compress a spring, it pushes back, and when you stretch it, it pulls back.
Several factors contribute to the extent of compression a spring experiences when a stone is dropped on it. Let's explore these crucial variables:
To calculate the compression of the spring, we can use Hooke's Law and the principle of conservation of energy. At the moment the stone hits the spring, the stone has potential energy due to its height, and this potential energy is converted into kinetic energy as the stone falls. As the stone compresses the spring, the kinetic energy is converted into elastic potential energy stored in the spring.
Here's how you can determine the compression:
Springs are ubiquitous in our world, playing crucial roles in countless machines, devices, and systems. Here are a few examples to illustrate their versatility:
Understanding how far a stone will compress a spring unveils the fundamental principles of physics that govern our world. It's a seemingly simple scenario that reveals the intricate relationship between force, displacement, and energy. Springs, with their remarkable ability to store and release energy, are essential components in numerous applications, making them indispensable in our daily lives.
So next time you see a spring, take a moment to appreciate its hidden power and the intricate interplay of forces that bring it to life. It's a small but mighty device, and its story is a testament to the elegance and beauty of physics.
Browse some of the custom wire forms and springs that we manufacture. Don’t see what you need? We specialize in made-to-order products that meet your application requirements.
Visit Our GalleryNeed a custom wire form or coil spring? We make it work. Fill out the contact form and a representative will respond within 1 business day. If you have a PDF or CAD file, you can submit to request a quote.