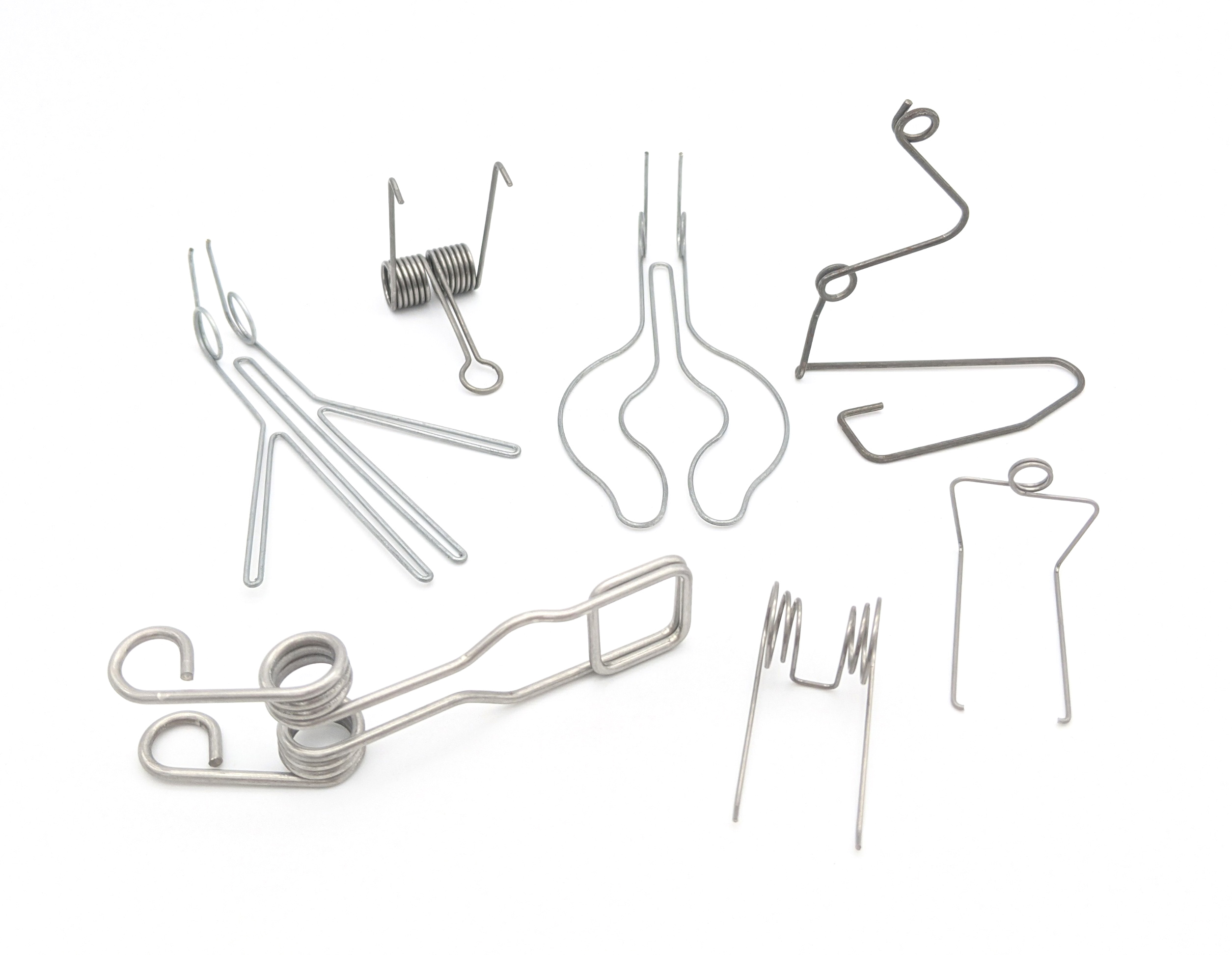
Get unique, complex parts easily. No matter your requirements, Chaoyi Spring creates hard-to-produce coil springs and wire forms.
Let us help you create the custom wire form you need, from S-hooks and J-hooks to utility hooks and more.
We work closely with customers across a wide range of industries, helping them design and manufacture made-to-order parts.
Why choose Chaoyi Spring? We prioritize customer-focused collaboration, modern equipment and the latest technology to make your parts per print.
Find the information and guidance you need, from measuring a spring to learning about materials, placing an order and much more.
Have you ever wondered how a simple spring can store and release energy so efficiently? The secret lies in the fascinating world of spring compression. This article delves into the


Have you ever wondered how a simple spring can store and release energy so efficiently? The secret lies in the fascinating world of spring compression. This article delves into the fundamental formula used to calculate compression in springs, exploring the key factors that influence this phenomenon. From Hooke's Law to the nuances of spring design, we'll embark on a journey to understand the mechanics behind this ubiquitous force.
The foundation of understanding compression in springs is Hooke's Law, a principle named after the brilliant English physicist Robert Hooke. This law states that the force exerted by a spring is directly proportional to its displacement from its equilibrium position. In simpler terms, the more you compress a spring, the greater the force it pushes back with.
Mathematically, Hooke's Law is expressed as: F = -kx, where:
The negative sign indicates that the force exerted by the spring is opposite in direction to the displacement. This means that if you compress the spring (positive displacement), the spring will push back with a force in the opposite direction (negative force).
The spring constant (k) is a crucial factor in the compression formula. It embodies the spring's resistance to deformation. A higher spring constant means a stiffer spring, requiring more force to compress it to a given length. Conversely, a lower spring constant signifies a more flexible spring, easier to compress. The spring constant is determined by the material used, the spring's geometry (wire diameter, number of coils, etc.), and the manufacturing process.
To determine the compression (Δx) of a spring subjected to a given force (F), we can rearrange Hooke's Law as follows:
Δx = F / k
This equation tells us that the compression of a spring is directly proportional to the applied force and inversely proportional to the spring constant.
While Hooke's Law provides a fundamental understanding of compression, several other factors come into play in real-world scenarios:
The principle of spring compression is ubiquitous in various fields, from everyday objects to sophisticated engineering systems. Here are some examples:
As technology continues to evolve, the design and application of springs are becoming more sophisticated. New materials, such as shape-memory alloys and carbon nanotubes, are being explored to create springs with enhanced properties like greater strength, flexibility, and resistance to fatigue. Advances in computer modeling and simulation are enabling engineers to optimize spring designs for specific applications, further expanding their range of possibilities.
In conclusion, the formula for compression in a spring, derived from Hooke's Law, provides a fundamental understanding of this vital phenomenon. While the basic principle is straightforward, the nuances of spring design, material properties, and environmental factors add complexity and intrigue to this seemingly simple concept. From automotive suspensions to medical devices and consumer products, spring compression plays a crucial role in our modern world. As technology advances, we can expect even more innovative applications of spring compression, pushing the boundaries of what's possible in various fields.
Browse some of the custom wire forms and springs that we manufacture. Don’t see what you need? We specialize in made-to-order products that meet your application requirements.
Visit Our GalleryNeed a custom wire form or coil spring? We make it work. Fill out the contact form and a representative will respond within 1 business day. If you have a PDF or CAD file, you can submit to request a quote.