Get unique, complex parts easily. No matter your requirements, Chaoyi Spring creates hard-to-produce coil springs and wire forms.
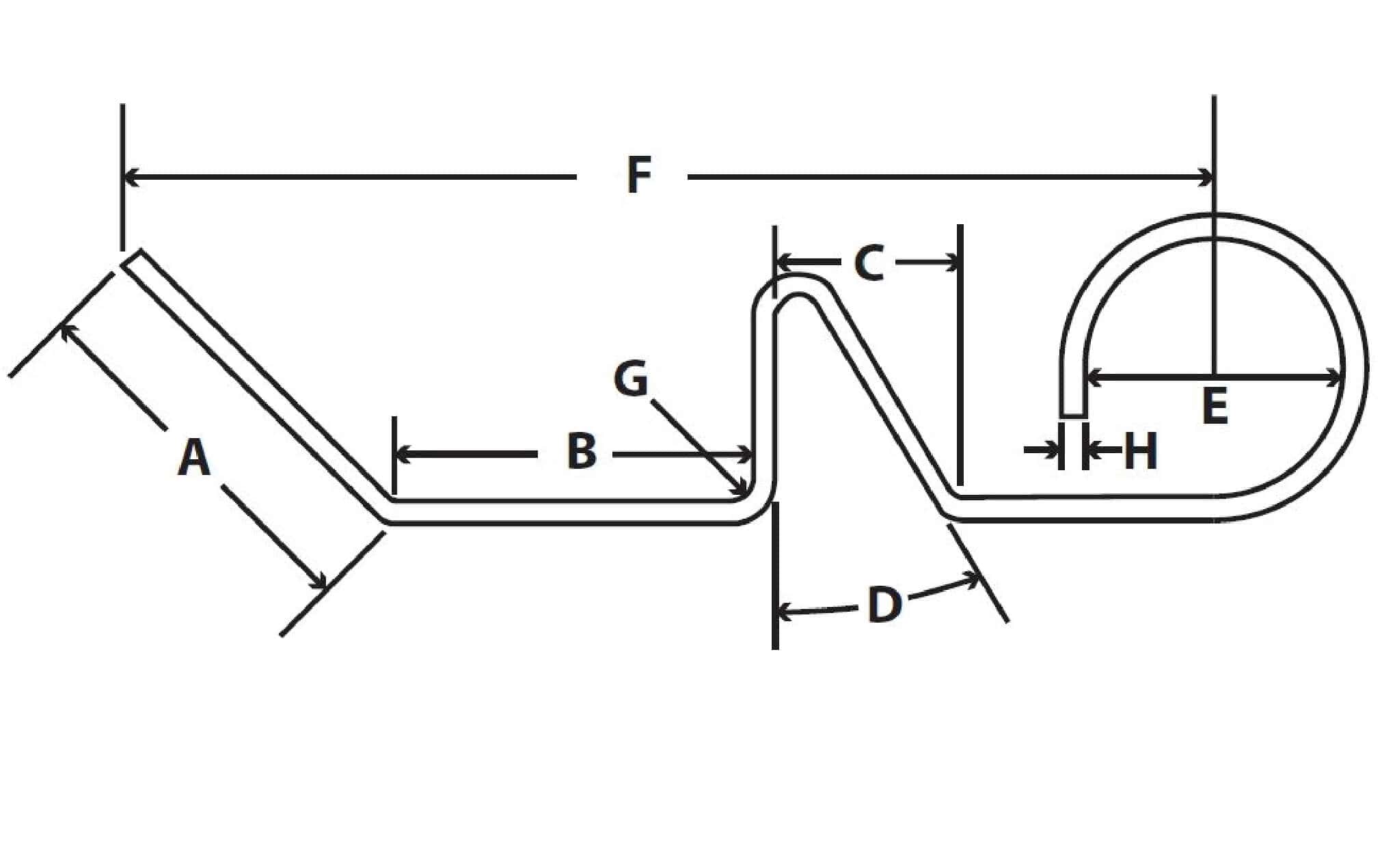
Let us help you create the custom wire form you need, from S-hooks and J-hooks to utility hooks and more.
We work closely with customers across a wide range of industries, helping them design and manufacture made-to-order parts.
Why choose Chaoyi Spring? We prioritize customer-focused collaboration, modern equipment and the latest technology to make your parts per print.
Find the information and guidance you need, from measuring a spring to learning about materials, placing an order and much more.
The spring compression formula, a fundamental concept in physics, serves as the bedrock for understanding how springs behave under applied forces. This formula, derived from Hooke's Law, quantifies the relationship
The spring compression formula, a fundamental concept in physics, serves as the bedrock for understanding how springs behave under applied forces. This formula, derived from Hooke's Law, quantifies the relationship between the applied force, the spring constant, and the resulting compression. By understanding this formula, we can predict the behavior of springs in various applications, from mechanical systems to everyday objects.
At its core, spring compression is the process of compressing a spring by applying an external force. This compression is directly related to the force applied, a principle encapsulated by Hooke's Law. Imagine a spring, like the ones found in a mechanical pencil or a car's suspension system. When you push on one end of the spring, it compresses, shortening in length. The amount of compression is directly proportional to the force you apply.
The spring compression formula, derived from Hooke's Law, mathematically expresses this relationship:
Force (F) = Spring Constant (k) x Compression (x)
This formula states that the force required to compress a spring is directly proportional to the spring constant (k) and the amount of compression (x). The spring constant, a property unique to each spring, represents its stiffness. A spring with a higher spring constant is stiffer and requires more force to compress it the same amount as a spring with a lower spring constant.
Spring compression, a seemingly simple concept, finds its application in a vast array of fields. Let's explore some key areas where understanding this principle is crucial:
In the realm of mechanical engineering, springs are ubiquitous. They serve as shock absorbers in vehicles, ensuring a smooth ride by absorbing and dissipating vibrations. Springs are also employed in various mechanical systems, like suspension bridges, where they contribute to structural stability.
The ubiquitous nature of springs extends beyond engineering. From the humble ballpoint pen to the sophisticated mechanisms in our smartphones, springs are integral components. The spring in a ballpoint pen retracts the writing tip when not in use, while springs in smartphones enable the tactile feedback we feel when pressing buttons.
The precision and sensitivity of springs make them ideal for medical applications. In medical devices like syringes, springs ensure controlled and accurate dispensing of medication. Springs also play a vital role in surgical instruments, aiding in delicate procedures.
The effectiveness of a spring in absorbing energy and providing support is contingent upon several key factors. Let's delve into some of these crucial aspects:
The spring constant, a measure of the spring's stiffness, directly impacts compression. A higher spring constant signifies a stiffer spring, requiring greater force to achieve the same compression. This parameter is typically determined experimentally by applying a known force and measuring the resulting compression.
The material from which a spring is made significantly influences its compression characteristics. Steel springs, known for their strength and durability, are commonly used in heavy-duty applications. Springs made from more flexible materials, like rubber or plastic, are often employed in situations requiring a softer spring response.
The physical dimensions of a spring, such as its length, diameter, and number of coils, contribute to its compression properties. A longer spring, with a larger number of coils, will generally compress more than a shorter spring with fewer coils.
Temperature plays a role in spring compression, although its effect is often less pronounced than other factors. A rise in temperature can lead to a slight reduction in spring stiffness, affecting the compression behavior.
The force applied to a spring directly determines the amount of compression. As the force increases, the compression increases proportionately, adhering to Hooke's Law.
While the spring compression formula provides a fundamental understanding of spring behavior, real-world scenarios can introduce complexities. In practice, springs can exhibit non-linear behavior, particularly when subjected to significant forces. Additionally, factors like fatigue and aging can influence a spring's performance over time.
To account for these nuances, more sophisticated models are employed in engineering analysis. These models often involve empirical data and numerical simulations to accurately predict spring behavior under various conditions.
Spring compression, while seemingly a simple concept, forms the foundation for countless technological advancements. It is the underlying principle behind a vast array of mechanical systems, everyday objects, and medical devices. Understanding this concept empowers us to design and optimize these systems, leading to innovation and efficiency across diverse fields.
Whether it's the smooth ride in a car, the precision of a surgical instrument, or the tactile feedback of our smartphones, spring compression plays a pivotal role in shaping our world. It's a testament to the power of simple scientific principles to drive complex technological advancements.
In conclusion, the spring compression formula is a powerful tool for understanding the behavior of springs under applied forces. From mechanical systems to everyday objects, this principle finds widespread application, driving innovation and efficiency across various fields. By comprehending the intricate relationship between force, spring constant, and compression, we can unlock the potential of springs and harness their remarkable properties to build a better future.
Browse some of the custom wire forms and springs that we manufacture. Don’t see what you need? We specialize in made-to-order products that meet your application requirements.
Visit Our Gallery
Need a custom wire form or coil spring? We make it work. Fill out the contact form and a representative will respond within 1 business day. If you have a PDF or CAD file, you can submit to request a quote.
Your Team For Innovative Wire Forming
We provide solutions for complex, high-quality
wire forms and coil springs.
©Dongguan Chaoyi Hardware Spring Co.
Dongguan, Guangdong, China, IL 523565
