Understanding the Compression of a Spring: A Deep Dive into Hookes Law

Have you ever wondered why a spring bounces back to its original shape after being compressed or stretched? The answer lies in a fundamental principle of physics known as Hooke's Law. This law describes the relationship between the force applied to a spring and its resulting deformation, providing a crucial framework for understanding the behavior of elastic materials. In this article, we'll delve into the intricacies of Hooke's Law, exploring its mathematical representation and its applications in various fields, from everyday objects to advanced engineering designs.

Hooke's Law: The Foundation of Spring Behavior

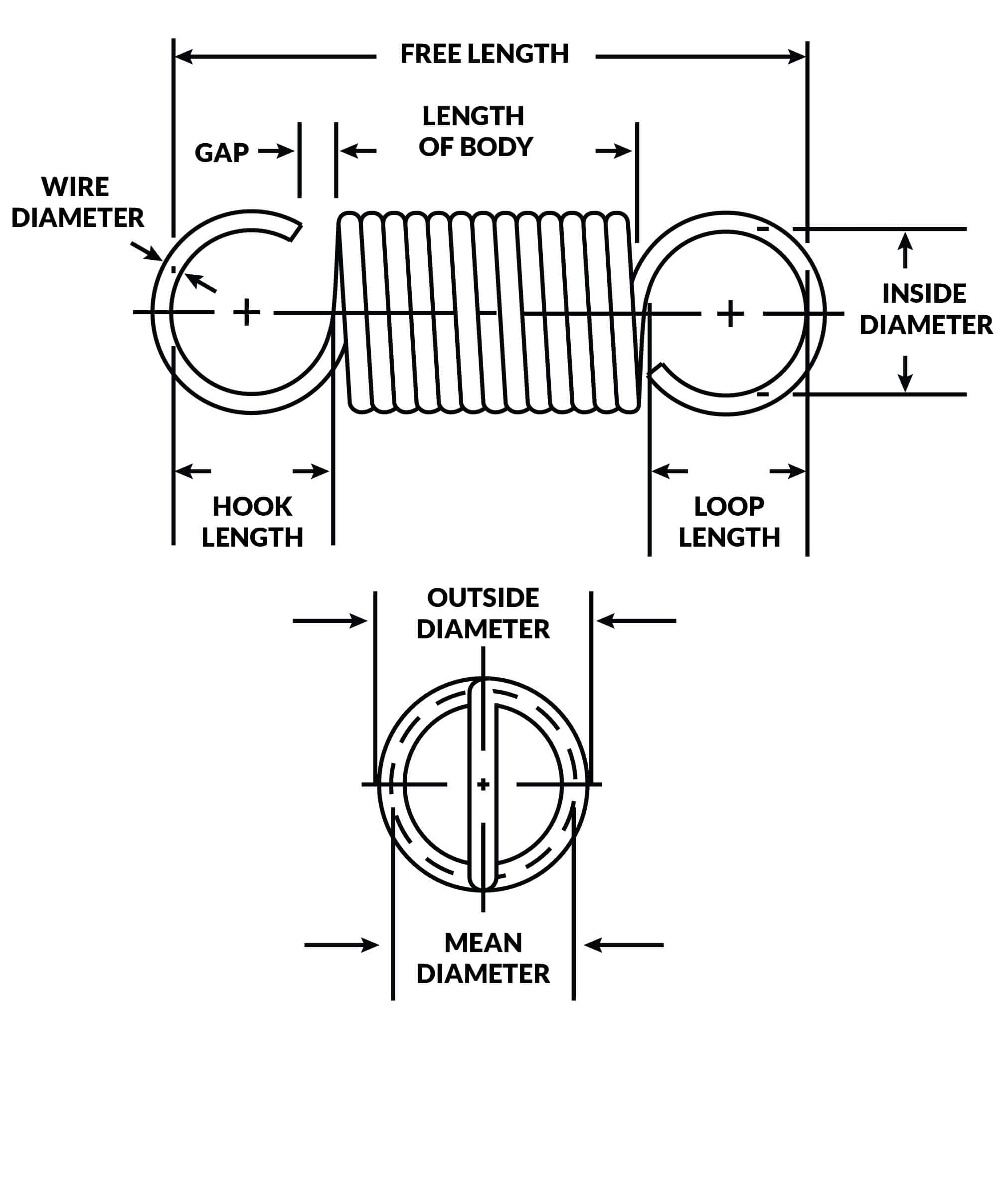
Imagine you have a spring and you start to compress it. You'll notice that the more you push, the harder it becomes to compress it further. This resistance to compression is directly proportional to the amount of compression. This relationship, beautifully encapsulated in Hooke's Law, states that the force required to compress or stretch a spring is directly proportional to the displacement from its equilibrium position.

Mathematically, Hooke's Law is expressed as:

F = -kx

Where:

• F is the force applied to the spring
• k is the spring constant, a measure of the stiffness of the spring
• x is the displacement from the equilibrium position

The negative sign indicates that the force exerted by the spring opposes the displacement. So, if you compress the spring (x is positive), the spring will exert a force pushing back (F is negative), and vice versa.

Understanding the Spring Constant

The spring constant, 'k', is a crucial parameter that defines the spring's stiffness. A higher spring constant means the spring is stiffer and requires a greater force to compress or stretch it. Imagine a heavy-duty spring used in a car suspension system versus a delicate spring found in a toy. The car suspension spring would have a much higher spring constant due to its need to withstand heavier loads.

The spring constant depends on the material of the spring, its geometry (like the wire diameter and the number of coils), and the way it's manufactured. Determining the spring constant experimentally involves measuring the force required to compress or stretch the spring by a known displacement.

Applications of Hooke's Law: From Simple to Complex

Hooke's Law might seem like a simple concept, but its applications are far-reaching and impact numerous aspects of our daily lives.

• Everyday Objects: From the spring in your pen to the shock absorbers in your car, Hooke's Law governs the behavior of countless everyday objects. Springs are used in a wide range of applications, including door closers, garage door openers, and even the mechanism that allows a retractable pen to extend and retract.
• Mechanical Systems: In various mechanical systems, springs are used to store and release energy. They are integral components in engines, where they help regulate valve timing, in clocks, where they control the oscillating movement, and in countless other machines.
• Civil Engineering: Hooke's Law plays a crucial role in civil engineering, particularly in structural design. Engineers use this principle to design bridges, buildings, and other structures that can withstand the stresses and strains imposed upon them by external forces.
• Medical Devices: Springs are found in a wide range of medical devices, from surgical instruments to medical implants. For example, springs are used in surgical clamps to provide a consistent grip and in orthodontic braces to apply gentle pressure to teeth.

Beyond the Ideal Spring: Limitations of Hooke's Law

While Hooke's Law provides a fundamental understanding of spring behavior, it's important to acknowledge its limitations. Real-world springs don't always behave perfectly according to this law, especially when subjected to extreme conditions.

Elastic Limit: Hooke's Law holds true only within the elastic limit of the spring material. Beyond this limit, the spring experiences permanent deformation and may not return to its original shape. Think about bending a paperclip – you can bend it back and forth a few times, but after a certain point, it'll stay bent.

Non-Linearity: Some springs exhibit non-linear behavior, meaning the force required to compress or stretch them isn't directly proportional to the displacement. This occurs when the material properties of the spring change under stress.

The Importance of Understanding Compression: A Real-World Example

Let's consider a practical example to highlight the importance of understanding spring compression: Imagine you're designing a shock absorber for a car. You need to ensure the shock absorber can absorb the impact of bumps and potholes without causing excessive vibrations or damage to the car. This involves carefully selecting a spring with the right spring constant to provide appropriate resistance to compression.

If the spring constant is too low, the shock absorber will compress too much, resulting in a bouncy ride. On the other hand, if the spring constant is too high, the shock absorber will be too stiff, leading to a jarring ride and potential damage to the car's suspension. This example illustrates the crucial role of spring compression and its impact on various engineering designs.

Exploring the Future: Beyond Hooke's Law

As technology advances, we are developing new materials and techniques that go beyond the limitations of traditional spring systems. For example, researchers are exploring shape-memory alloys that can remember their original shape and return to it after being deformed. These advancements are paving the way for more innovative and efficient spring-like systems with enhanced performance and functionality.

In conclusion, understanding the compression of a spring is crucial in various fields, from simple everyday applications to complex engineering designs. Hooke's Law provides a fundamental framework for grasping the relationship between force and displacement in elastic materials. While it's essential to recognize the limitations of this law, particularly under extreme conditions, it remains a cornerstone in understanding the behavior of springs and their widespread applications. As we continue to explore and innovate, we can expect to see even more fascinating applications of spring compression in the future, shaping our world in remarkable ways.